Polkadot state trie storage in Gossamer
Dive into Polkadot's state trie storage with Gossamer! Learn why tries matter for blockchain integrity, how Merkle trees help in data verification, and the unique challenges Gossamer addresses.

Suppose we have a file that we want to store or send remotely while still being able to retrieve it later.
An easy solution would be to send files in a way that allows us to query for them later. However, this causes some issues as there is no way to verify that the retrieved file is the same as the file we originally sent.
Data integrity
To verify the integrity of a receiving file and ensure it hasn't been modified, we can generate a digest d, also known as a unique cryptographic representation of the file.
For example, by hashing the file 𝐹 so 𝑑 = 𝐻(𝐹), then we can store this digest locally in our device, send the file, and when we receive the new file, we can generate a new digest 𝑑′ = 𝐻(𝐹′)
After that, if the digests are equal, 𝑑 = 𝑑′ = 𝐻(𝐹) = 𝐻(𝐹′), we can be sure that the file is the same as the one we sent, without tampering.
This process is easy to perform if we only send a single file. However, if we need to check multiple files, it must store digests for each file in the list.

This process is easy to perform if we only send a single file. However, if we need to check multiple files, it must store digests for each file in the list.
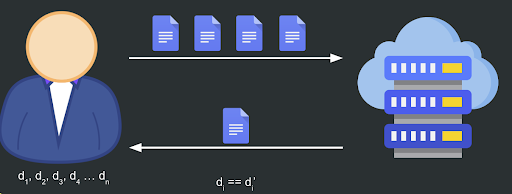
Now, that’s when it stops being practical. As the storage requirements overwhelm the system, we must find a way to store a constant-sized digest.
Luckily, Merkle trees provide an elegant solution.
Merkle trees
By hashing each file and combining these hashes into a single root hash, Merkle trees ensure the integrity of multiple files in a single digest called the trie root 𝑅, significantly reducing the storage space needed on local devices.

Merkle proof
To verify a file using a Merkle tree, we need to define a new way to prove membership, called Merkle proof 𝜋.
So every time we receive a file, instead of being on the user to calculate the membership proof, they will receive the file along with proof of membership 𝜋𝑖 for that file 𝐹𝑖.
Then we can verify 𝐹𝑖 based on the digest 𝑅 we stored locally using the Merkle proof 𝜋𝑖.
For example, if we want to check that the file 𝐹2 we received hasn't gotten modified, we can build a partial trie hashing up the tree along the path from the leaf 𝐹2 using the hash for the 𝐹2 file 𝐻(𝐹2) and using the nodes contained in the proof 𝜋2

Once the new Merkle root 𝐷𝑅 gets computed, we can check that 𝐷𝑅=𝑅. If it is true, we can ensure that the file 𝐹2 is the expected file.
Pros & cons
Merkle trees are efficient to construct. A Merkle tree over 𝑛 files can be built in 𝑂(𝑛) time. However, the proof 𝜋 might become too large in some cases.
For instance, if we have a binary tree with 230 ≈ 109 leaves, the tree depth will be approximately 30. Since a Merkle tree contains one node at each level, the Merkle proof will be roughly 1KB if we use 256-bit hashes. This could become impractical if we have many small files or, in the case of a blockchain, a high number of small transactions.
Improvements
One naive way to reduce the size of our proofs is to reduce the height of the resulting tree. As we mentioned, in a binary Merkle tree, the proof consists of one node per level, so to reduce the size, we might increase the branching factor.
If we have a Merkle tree with a branching factor of 𝑘, the height will be improved by a 𝑙𝑜𝑔2𝑘 factor from 𝑙𝑜𝑔2𝑛 to 𝑙𝑜𝑔𝑘𝑛.
Still, the problem with this approach is that the Merkle proof continues to grow larger, from 𝑂(𝑙𝑜𝑔2𝑛) to 𝑂(𝑘𝑙𝑜𝑔𝑘𝑛), since our proof will consist in (𝑘−1) nodes per level instead of only one node per level.
Another way to improve this is to use a radix trie instead of regular trees. By doing that, we can compress the nodes that share the same prefix into the same node.
Keep this in mind because we are going to use it later!
Usage in blockchain
Merkle tries are widely used in blockchain since they help us verify our storage integrity.
For example, when we are downloading and validating blocks, we need to ensure the data integrity:
- We receive a new bloc. The block header contains a Merkle root of the storage.
- After applying these block transactions, we use the duplicate transactions in our storage.
- We then create a Merkle trie using that storage data.
- Afterward, we can check if the block is valid by comparing our Merkle trie hash with the one in the block header. If they match, the block is valid, and we can add it to our blockchain and propagate it to the other peers.
Polkadot state storage trie
The blockchain state in Polokadot is stored in System Storage, which is basically a key-value store (KVS) database.
The Polkadot specification mandates the use of a radix-16 trie to reorganize the stored data, enabling the consistent and efficient computation of the Merkle hash 𝐻𝑟 for the entire or part of the state storage.
Keys
We use a radix-16 trie because we are going to encode the storage keys in a special way where each storage key byte (8 bits) is split into nibbles (4 bits) to represent values in the range [0,𝐹]
$$
KeyEncode : B \rightarrow Nibbles^4
$$
$$
k \rightarrow (k_{enc1},...,k_{enc1})
$$
$$
(b_1,...,b_n) \rightarrow (b^1_1, b^2_1, b^1_2, b^2_2,..., b^1_n, b^2_n)
$$
For example, if the key is:
Key := "gossamer".
The bytes will be:
KeyBytes = []byte{0x67, 0x6f, 0x73, 0x73, 0x61, 0x6d, 0x65, 0x72}
So each nibble will be:
0x6 0x7 0x6 0xf 0x7 0x3 0x6 0x1 0x6 0xd 0x6 0x5 0x7 0x2
By doing this, we can easily traverse the radix trie to reach the node identifying the storage value of 𝑘
Merkle value
Since this is a Merkle trie, we must calculate the Merkle value for a given node 𝑁, denoted as 𝐻(𝑁). It is defined as follows:

The Merkle value of each node should depend on the Merkle value of its children and its own data.
Trie traversing
Since the keys are nibbles, we can easily traverse the trie by defining a target key and consuming the keys we are visiting. When we reach a node whose partial key is equal to the remaining key we have, we can say that we have reached the node we were looking for.
Node value
Each node 𝑁 gets encoded in a special way called node value 𝑣𝑁, consisting of the following concatenated data
$$
v_N = Head_N || Enc_{HE}(pk_N) || sv_N
$$
Node header
The Head𝑁 is defined as follows:
| Header | Node Type |
|---|---|
| 01 | Leaf |
| 10 | Branch without value |
| 11 | Branch with value |
| 001 | Leaf with hashed subvalue (trie V1) |
| 0001 | Branch with hashed subvalue (trie V1) |
| 00000000 | Empty |
Encoded partial key
The EncHE(𝑝𝑘𝑁) is the hexadecimal representation of the nibbled partial key. In other words, it’s the inverse function of:
$$
KeyEncode : B \rightarrow Nibbles^4
$$
So it is defined as:
$$
Enc_{HE}(pk_N) : Nibbles^4 \rightarrow B
$$
Node subvalue
Each node 𝑁 could contain a value called subvalue referred to as 𝑠𝑣𝑁, defined as follows:
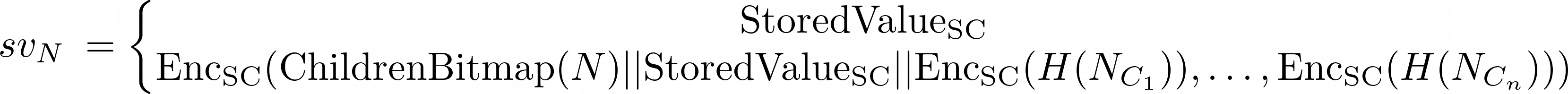
The first variant is a leaf node, and the second is a branch node.

This 𝑠𝑣𝑁 could be empty in case the node 𝑁 doesn’t contain a value (for example, for branches without values) or an EncSC(StoredValue(𝑘𝑁)) in the case it does include a value.
Note: There is a special case when we are using trie V1, where the value is not encoded but hashed and stored directly in the node to increase performance. We will have a mapping in our underlying database to get the raw value if needed.
Child Tries
Child tries are a special type of trie that exist as part of a main trie but operate within their own isolated environment. The main state trie relies on them by storing a node (𝐾𝑁,𝑉𝑁) corresponding to an individual child trie.
Differences between v0 and v1
Something worth mentioning is the difference between the first version of the Polkadot trie (V0) and the second (V1).
Some improvements were added as part of V1 to improve the trie's performance.
In an effort to save memory and prevent executing expensive hash calculations, the node subvalues 𝑠𝑣𝑁 greater than 32 bytes get hashed. This hash is then stored as part of the node instead of using the EncSC(StoredValue(𝑘𝑁))

Gossamer implementation
Our current implementation uses an in-memory Merkle trie with an underlying database where we can store and load the data.
Node definition
A simple node is sufficient to represent the root of the trie and all its children. Some shared and specific fields are used when the node is a leaf or a branch. Additionally, there are some internal fields and struct methods that are omitted in this example:

Trie definition
Given a root node, we can build a trie. We also need a mapping to store and access its child tries, which are also InMemoryTrie.
If we combine this with a few other methods, it should be enough to easily manage all trie operations.

Forks management
Since each forked chain will have a different and independent trie, it's important to maintain the mapping between them so that they can handle fork management efficiently
Pros & Cons
While Gossamer is a complete implementation, the team still identifies some areas where we are able to improve.

Future improvements
We are currently working to address these drawbacks by making a major change in how our trie operates.
The main change is transitioning from a pre-loaded in-memory trie to a lazy-loading trie. This will help improve both memory usage and startup time.
But that's something for a different post. Stay tuned for the second part, where we will discuss the transition from the in-memory trie to the new lazy-loading trie and provide benchmarks showing the improvements.
More Gossamer
- Chat directly with the team → Discord
- Learn more by checking out the → Docs
- Keep a tab on the progress → Twitter
Interested in joining the team? Have a background in protocol engineering? Check out the job opening below 👇

About ChainSafe
ChainSafe is a leading blockchain research and development firm specializing in protocol engineering, cross-chain interoperability, and web3 gaming. Alongside its contributions to major ecosystems such as Ethereum, Polkadot, and Filecoin, ChainSafe creates solutions for developers across the web3 space utilizing expertise in gaming, interoperability, and decentralized storage. As part of its mission to build innovative products for users and improved tooling for developers, ChainSafe embodies an open-source and community-oriented ethos to advance the future of the internet.





